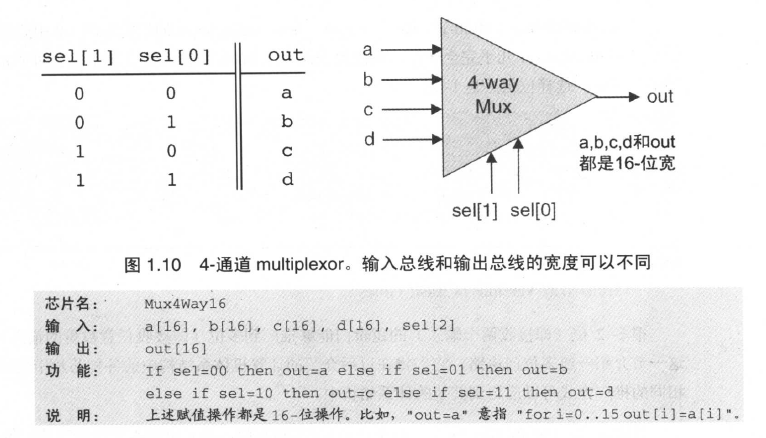
几个特殊的语法, 记录在最上面 , 免得到时候忘记 CPU can only execute programs stored in instruction memory
1
2
3
1. Add16(a=in, b[0]=true,b[1..15]=false, out=out);
2. Mux16(a=f3, b=no1, sel=no, out=out ,out = no3);
3. Mux16(a=o2, b=false, sel=reset, out=o3); // 16位直接置零 b=false
布尔函数
所有“两变量”的函数值。 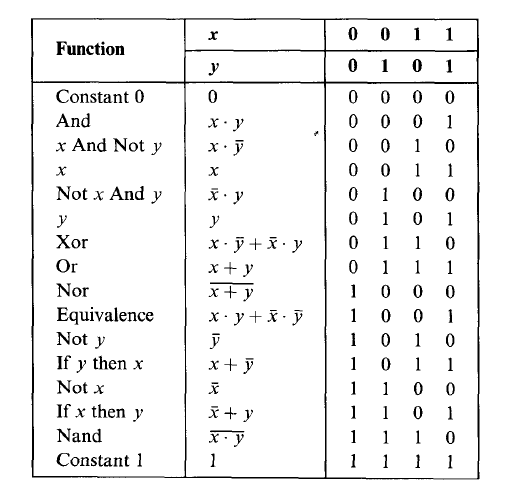 And/Or/Not都可以只用Nand或者Nor来表示,那么所有的布尔函数都可以只用Nand或者Nor来表示。一旦物理上实现了Nand功能,就可以来构建
And/Or/Not都可以只用Nand或者Nor来表示,那么所有的布尔函数都可以只用Nand或者Nor来表示。一旦物理上实现了Nand功能,就可以来构建
常见的几种门
基本门
- Nand 门
1
a and b 取反
Not 门
And 门
Or门
Multiplexor门 (选择器)
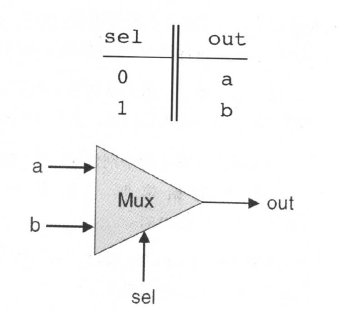 sel 位为选择位
sel 位为选择位
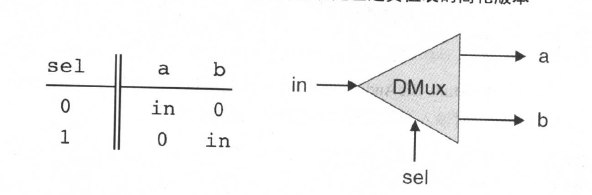
- Demnultiplexor 与multiplexor 相反
只有一个输出变量,sel 选择到底哪个通道输出。
多位基本门
通用计算机要求设计在多为数据线(总线)上运行。
多为Not 对它的n位输入总线上的每一位取反,然后再输出。
多位And 对两个n位输入总线上对应的每一对输入变量进行and操作,然后输出。
多位Or 对两个n位输入总线上对应的每一对输入变量进行or操作,然后输出。
多位Multiplexor 与单位的基本类似。sel = 0 or sel = 1
多通道逻辑门
很多两位的逻辑门能推广到多位的逻辑门(即接受任意数量的输入)
多通道or 一位及以上为1,则为1,否则为0.
多通道/多位 Multiplexor 一个拥有m个通道,每个通道的数据宽度为n,将m个n位输入变量中选择一个并从其单一的n位输入总线上输出。 sel 选择位等于 以2 为底的 m 对数。

多通道Demultiplexor 与上述相反。 从m个可能的n位输出通道中选择输出一个n位的输入变量。
门的实现
And门
1
2
3
4
5
6
7
8
9
10
11
CHIP And {
IN a, b;
OUT out;
PARTS:
// Put your code here:
Nand(a=a, b=b, out=w1);
Nand(a=a, b=b, out=w2);
Nand(a=w1, b=w2, out=out);
}
And16
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
CHIP And16 {
IN a[16], b[16];
OUT out[16];
PARTS:
// Put your code here:
And(a=a[0], b=b[1], out=out[0]);
And(a=a[1], b=b[2], out=out[1]);
And(a=a[2], b=b[3], out=out[2]);
And(a=a[3], b=b[4], out=out[3]);
And(a=a[4], b=b[5], out=out[4]);
And(a=a[5], b=b[6], out=out[5]);
And(a=a[6], b=b[7], out=out[6]);
And(a=a[7], b=b[8], out=out[7]);
And(a=a[8], b=b[9], out=out[8]);
And(a=a[9], b=b[10], out=out[9]);
And(a=a[10], b=b[11], out=out[10]);
And(a=a[11], b=b[12], out=out[11]);
And(a=a[12], b=b[13], out=out[12]);
And(a=a[13], b=b[14], out=out[13]);
And(a=a[14], b=b[15], out=out[14]);
And(a=a[15], b=b[15], out=out[15]);
}
DMux
1
2
3
4
5
6
7
8
9
10
11
12
// 选择器
* {a, b} = {in, 0} if sel == 0
* {0, in} if sel == 1
CHIP DMux {
IN in, sel;
OUT a, b;
PARTS:
Not(in = sel, out = n1);
And(a = in, b = n1, out = a);
And(a = in, b = sel, out = b);
}
DMux4Way
本质上来说,就是一个选择器。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
/**
* 先根据第二位选,再根据第一位选
* sel 位从右往左边读
* 4-way demultiplexor:
* {a, b, c, d} = {in, 0, 0, 0} if sel == 00
* {0, in, 0, 0} if sel == 01
* {0, 0, in, 0} if sel == 10
* {0, 0, 0, in} if sel == 11
* 从上述代码可以发现 ab 的第二位都是 0,cd 的第二位都是 1
* 利用这一特性先对 sel 的第二位进行一个 DMux 操作
* 如果第二位是 0,它只有两种可能:ab,如果是 1,则是 cd
* 然后再对 sel 的第一位进行操作,对于 ab 来说,第一位为 0 则是 a,否则为 b
* 对于 cd 来说,第一位为 0 则是 c,否则为 d
*/
CHIP DMux4Way {
IN in, sel[2];
OUT a, b, c, d;
PARTS:
DMux(in=in, sel=sel[1], a=l1, b=l2);
DMux(in=l1, sel=sel[0], a=a, b=b);
DMux(in=l2, sel=sel[0], a=c, b=d);
}
DMux8Way
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
// 以二位的选择器构建
CHIP DMux8Way {
IN in, sel[3];
OUT a, b, c, d, e, f, g, h;
PARTS:
// Put your code here:
DMux(in=in, sel=sel[2], a=m1, b=m2);
DMux(in=m1, sel=sel[1], a=s1, b=s2);
DMux(in=s1, sel=sel[0], a=a, b=b);
DMux(in=s2, sel=sel[0], a=c, b=d);
DMux(in=m2, sel=sel[1], a=f1, b=f2);
DMux(in=f1, sel=sel[0], a=e, b=f);
DMux(in=f2, sel=sel[0], a=g, b=h);
}
// 以 四位的选择器构建
CHIP DMux8Way {
IN in, sel[3];
OUT a, b, c, d, e, f, g, h;
PARTS:
DMux4Way(in = in, sel = sel[1..2], a = o1, b = o2, c = o3, d = o4);
DMux(in = o1, sel = sel[0], a = a, b = b);
DMux(in = o2, sel = sel[0], a = c, b = d);
DMux(in = o3, sel = sel[0], a = e, b = f);
DMux(in = o4, sel = sel[0], a = g, b = h);
}
Mux
1
2
3
4
5
6
7
8
9
10
11
// 不知道这个叫啥 反选择器 ?
CHIP Mux {
IN a, b, sel;
OUT out;
PARTS:
And(a=b, b=sel, out=o1);
Not(in=sel, out=notsel);
And(a=a, b=notsel, out=o2);
Or(a=o1, b=o2, out=out);
}
一点总结 Mux16 与 Mux8way16 区别
- 不管是 Mux16 Or16 Not16 都可以看作是一位门的扩展,仅此而已。
- 而Mux8way16 与 Or8Way16 前面的一个数字代表多少个 后一位数字代表每个的位数。
- = =